↜ Back to index Introduction to Numerical Analysis 2
Part b–Lecture 8
Report 2
Submit the solutions to the following problems to LMS (Report 2) by Monday 2/14 (strict deadline).
Problem 1. (30 points) “Dirichlet boundary condition”
Recall the program that we made in Lecture b7.
Modify the program to print the values of the solution x as in Report 1, Problem 2 and make the following plots of the solution x similarly to Report 1, Problem 2 example.
Use the following updated gnuplot commands:
set title '123456789'
unset key
set contour base
set cntrparam levels 50
set hidden3d
splot 'out.txt' matrix with linesNote set hidden3d to make the plot easier to understand!
Always use q = 127, \varepsilon = 10^{-10} and \omega = 1.9 in the preconditioner.
Use b_i = \begin{cases} 1, & i \leq q,\\ 0, & \text{otherwise}. \end{cases}
Submit the plot with your student ID as the title. 問1
Use b_i = \begin{cases} 1, & i \geq n - q,\\ 0, & \text{otherwise}. \end{cases}
Submit the plot with your student ID as the title. 問2
Use b_{q (i - 1) + j} = \exp \left(-100\left(\left(\tfrac{i}{q+1} - \tfrac 12\right)^2 + \left(\tfrac{j}{q+1}-\tfrac 12\right)^2\right)\right), \qquad i, j = 1, \ldots, q.
Submit the plot with your student ID as the title. 問3
Problem 2. (35 points) “Periodic boundary condition in i”
Modify the program in Problem 1 to read q from the input and print the solution for the matrix A_{ij} = \begin{cases} 4, & i=j,\\ -1, & \Big(|i - j| = 1 \text{ and } \min(i,j) \neq 0 \mod q\Big) \text{ or } |i-j| = q \text{ or } |i - j| = n - q,\\ 0, & \text{otherwise} \end{cases} and b_i = 1/(q+1)^2. Use \varepsilon = 10^{-10} and \omega = 1.9 in the preconditioner.
Be careful about the order of nonzero elements in each row.
- Submit the code. (15 points) 問4
For input q = 127, plot the solution x as in Problem 1.
Submit the plot with your student ID as the title. 問5
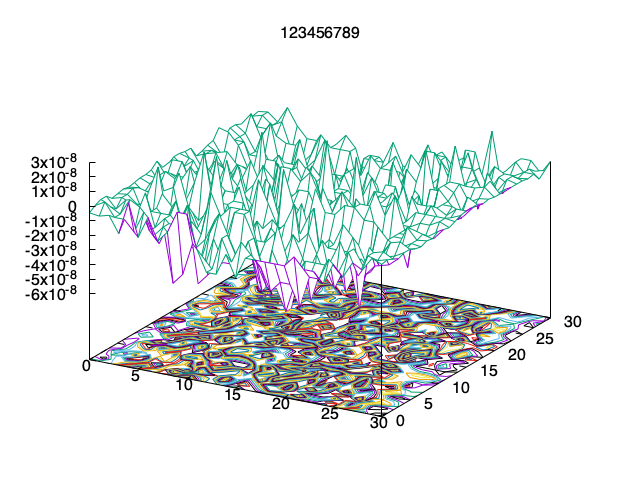
In the same way, plot the difference x-y between the solution x, and the expected exact solution y defined as y_{q (i - 1) + j} = \tfrac{j}{2(q+1)}\big(1 - \tfrac{j}{q+1}\big), \qquad i, j = 1. \ldots, q.
The value should be very close to 0.
Submit the plot with your student ID as the title. 問6
Problem 3. (35 points) “Periodic boundary condition in j”
As in Exercise 2, modify the program to find the solution for the matrix A_{ij} = \begin{cases} 4, & i=j,\\ -1, & \left\{ \begin{aligned} &\Big(|i - j| = 1 \text{ and } \min(i,j) \neq 0 \mod q\Big)\\ \text{ or } &\Big(|i - j| = q - 1 \text{ and } \min(i,j) = 1 \mod q\Big)\\ \text{ or } &|i - j| = q, \end{aligned} \right. \\ 0, & \text{otherwise}, \end{cases} and b_i = 1/(q+1)^2. Use \varepsilon = 10^{-10} and \omega = 1.9 in the preconditioner.
- Submit the code. (15 points) 問7
For input q = 127, plot the solution x as in Problem 1.
Submit the plot with your student ID as the title. 問8
In the same way, plot the difference x-y between the solution x, and the expected exact solution y defined as y_{q (i - 1) + j} = \tfrac{i}{2(q+1)}\big(1 - \tfrac{i}{q+1}\big), \qquad i, j = 1. \ldots, q.
The value should be very close to 0.
Submit the plot with your student ID as the title. 問9
Example solutions
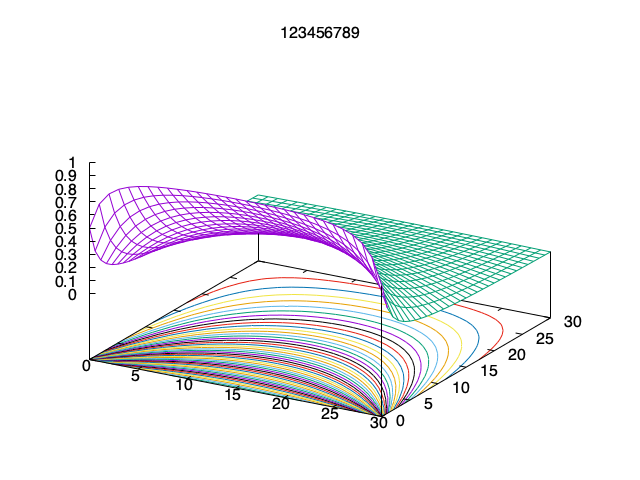
Problem 1 examples
1 (q = 31)
Problem 2 examples
2 (q = 31)
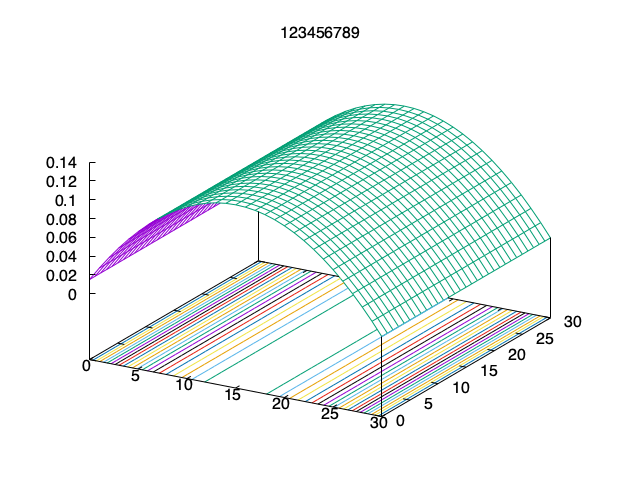
3 (q = 31)